https://www.acmicpc.net/problem/1629
이번 문제는 분할 정복 개념을 공부하기 위해 백준 알고리즘의 단계별 문제 풀이에서 고른 성공률 25%의 곱셈이라는 문제입니다. 음.. 이 문제를 풀면서 느꼈던 것은 분할 정복의 개념 자체는 쉽지만 이 개념을 어떻게 적용하는지는 쉽지 않다는 것입니다. 마치, 고등학교 때 미적분 기본 개념들을 숙지해도 수능의 29, 30번 문제는 어떻게 푸는지 감이 잘 안잡히는... 그런 느낌이었습니다. 아이디어가 떠오르면 어떻게든 하면 되는데? 그 아이디어가 생각나기까지는 어느 정도 직관이 필요한 것 같습니다.
분할 정복이란?
분할 정복이란, 말 그대로 분할하고 정복하여 답을 구해내는 알고리즘 기법입니다. 당연한 말이잖아... 좀 더 풀어 설명하면, 주어진 문제가 너무 커서 바로 풀기는 시간이 오래 걸리거나 불가능할 때 이를 풀 수 있는 작은 문제들로 쪼개어 나중에 그 문제들을 합해 답을 구하는 문제 유형입니다. 이번 문제 곱셈은 분할 정복의 개념을 잘 보여주고 적용하기 좋은 문제입니다. 난이도 자체는 높지 않아 보이지만, 저 같은 경우는 분할 정복으로 푸는 법이 생각나지 않으니, 수학적으로 접근하려다가 시간을 좀 쓴 케이스가 되었네요.
Hint!
이 문제는 사실 힌트를 보면 끝나는 문제 같습니다. 그러니 이 문장을 보고 힌트를 보고 풀지 않을테야! 하는 오기있는 분이시라면 이 밑을 읽지 마세요 ㅎㅎ. 여기서 설명하는 `A`, `B`, `C`는 문제에서 정의한 것과 같습니다.
힌트는 제곱해야 하는 수, 즉, `B`를 적절히 변형해야 한다는 점입니다. 문제에서는 `B`의 값이 매우 큰 값까지 주어질 수 있으니 그대로 제곱을 했다가는 시간초과나 메모리 초과를 면할 수 없을겁니다. 그러니, 아래처럼 `B`를 2에 대한 거듭제곱 형태로 계속하여 분할하여 `B`만큼 `A`를 거듭제곱 하는 것이 아니라 제곱을 한 뒤, 거기에 제곱을 또하고 또하는 방식을 취하여 연산 수를 최대한 줄여볼 것입니다. 이 문제가 분할 정복의 한 문제로 소개된 이유를 아시겠죠?
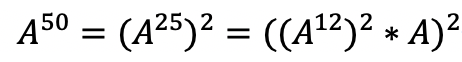
이 때, 두가지 경우가 있을 수 있는데요, 계속해서 2로 나누어 갈때 `B`가 짝수인 경우에는 나누어 떨어지니까 문제는 없는데 홀 수일 때는 나머지 하나가 남죠. 위의 식에서 제일 오른쪽의 경우처럼 말이에요. 그래서 `B`가 1이 되어 더이상 나눌 수 없을 때까지 2로 나누었을 때, 나머지가 없는 경우는 0을, 나머지가 1로 있는 경우는 1로 나누어서 어떻게 나누었는지 저장하는 리스트를 따로 만들어 주어야합니다. 그리고 이 리스트를 역순으로 정렬하여
- 1이 저장된 경우 `A`를 제곱한 뒤 `A`를 한 번더 곱하고,
- 0이 저장된 경우 그냥 `A`를 제곱하면 됩니다.
가령, 12가 `B`로 주어졌으면, 빈 리스트인 `multi_form`을 만들고
- 12 // 2 = 6이고 나누어 떨어졌으니 0을 `multi_form`에 `append` (//는 몫을 구하는 연산자입니다.)
- 6 // 2 = 3이고 나누어 떨어졌으니 0을 `multi_form`에 `append`
- 3 // 2 = 1이고 나머지가 1이니 1을 `multi_form`에 `append`
즉 리스트는 `[0, 0, 1]`이 저장이 되었을테고 이를 역배열하여 `[1, 0, 0]`을 만든 뒤, 위의 규칙처럼 `A`에 순서대로 곱해주면 되는 것입니다. 그러면 결과적으로 A^12 가 되겠죠?
하지만, 이렇게 진행을 해도 A^B의 결과로 수가 너무 커질 것을 생각한다면, 역시 메모리 초과가 일어날 수 있습니다. 그래서 역배열된 multi_form의 순서대로 제곱을 해줄 때마다 `C`로 계속해서 나누어 줄겁니다. 그러면 수가 계속해서 커지는 것을 막을 수 있고, 제곱이 되기 전에는 항상 C의 나머지니까 C보단 작아질 겁니다. 그래도 똑같냐고요? 네 똑같습니다. 어떤 수를 제곱하고 `C`로 나누나, 제곱하기 전에 `C`로 나눈 뒤 제곱을 하고 다시 `C`로 나누어도 같습니다(????). 말이 좀 이상한데 정리하면 아래와 같이 됩니다.

음, 이걸 여기에 증명하거나 설명하기는 조금 길어질 것 같아서 생략을 할게요. 대신에 `A`, `B`, `C`를 적절히 설정해서 손으로 몇 문제 풀어보시면 이해가 갈겁니다. 나머지를 구할 때, 나누어 떨어진 부분들에 대해서는 아예 연산에서 제외되는 그런 상황이라고 생각하시면 직관적일 것 같습니다.
아래의 코드로 성공했습니다. 코드가 길지 않고 어렵지 않으니, 어떻게 작동되는지는 가져다가 궁금한 위치에 print해보셔서 확인하시면 더 도움될 것 같습니다.
A, B, C = map(int, input().split())
multi_form = []
while True:
if B == 1: break
if B % 2 == 0: multi_form.append(False)
else: multi_form.append(True)
B = B // 2
# 자주 쓰이는 연산이니 따로 변수로 저장
D = A % C
result = D
for form in multi_form[::-1]:
if form: result = result ** 2 * (D)
else: result = result ** 2
result = result % C
print(result)
'Python > 백준 알고리즘' 카테고리의 다른 글
| [백준 알고리즘: python 3] #1027 - 고층 건물 (1) | 2020.04.18 |
|---|---|
| [백준 알고리즘: python 3] #1026 - 보물 (0) | 2020.04.14 |
| [백준 알고리즘: python 3] #10951 - A + B - 4 (0) | 2020.04.06 |
| [백준 알고리즘: python 3] #1931 - 회의실 배정 (Greedy 알고리즘 스터디) (0) | 2020.04.02 |
| [백준 알고리즘: python 3] #2178 - 미로탐색(BFS 스터디) (0) | 2020.03.25 |
https://www.acmicpc.net/problem/1629
이번 문제는 분할 정복 개념을 공부하기 위해 백준 알고리즘의 단계별 문제 풀이에서 고른 성공률 25%의 곱셈이라는 문제입니다. 음.. 이 문제를 풀면서 느꼈던 것은 분할 정복의 개념 자체는 쉽지만 이 개념을 어떻게 적용하는지는 쉽지 않다는 것입니다. 마치, 고등학교 때 미적분 기본 개념들을 숙지해도 수능의 29, 30번 문제는 어떻게 푸는지 감이 잘 안잡히는... 그런 느낌이었습니다. 아이디어가 떠오르면 어떻게든 하면 되는데? 그 아이디어가 생각나기까지는 어느 정도 직관이 필요한 것 같습니다.
분할 정복이란?
분할 정복이란, 말 그대로 분할하고 정복하여 답을 구해내는 알고리즘 기법입니다. 당연한 말이잖아... 좀 더 풀어 설명하면, 주어진 문제가 너무 커서 바로 풀기는 시간이 오래 걸리거나 불가능할 때 이를 풀 수 있는 작은 문제들로 쪼개어 나중에 그 문제들을 합해 답을 구하는 문제 유형입니다. 이번 문제 곱셈은 분할 정복의 개념을 잘 보여주고 적용하기 좋은 문제입니다. 난이도 자체는 높지 않아 보이지만, 저 같은 경우는 분할 정복으로 푸는 법이 생각나지 않으니, 수학적으로 접근하려다가 시간을 좀 쓴 케이스가 되었네요.
Hint!
이 문제는 사실 힌트를 보면 끝나는 문제 같습니다. 그러니 이 문장을 보고 힌트를 보고 풀지 않을테야! 하는 오기있는 분이시라면 이 밑을 읽지 마세요 ㅎㅎ. 여기서 설명하는 `A`, `B`, `C`는 문제에서 정의한 것과 같습니다.
힌트는 제곱해야 하는 수, 즉, `B`를 적절히 변형해야 한다는 점입니다. 문제에서는 `B`의 값이 매우 큰 값까지 주어질 수 있으니 그대로 제곱을 했다가는 시간초과나 메모리 초과를 면할 수 없을겁니다. 그러니, 아래처럼 `B`를 2에 대한 거듭제곱 형태로 계속하여 분할하여 `B`만큼 `A`를 거듭제곱 하는 것이 아니라 제곱을 한 뒤, 거기에 제곱을 또하고 또하는 방식을 취하여 연산 수를 최대한 줄여볼 것입니다. 이 문제가 분할 정복의 한 문제로 소개된 이유를 아시겠죠?
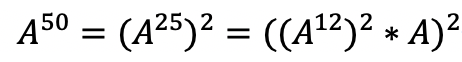
이 때, 두가지 경우가 있을 수 있는데요, 계속해서 2로 나누어 갈때 `B`가 짝수인 경우에는 나누어 떨어지니까 문제는 없는데 홀 수일 때는 나머지 하나가 남죠. 위의 식에서 제일 오른쪽의 경우처럼 말이에요. 그래서 `B`가 1이 되어 더이상 나눌 수 없을 때까지 2로 나누었을 때, 나머지가 없는 경우는 0을, 나머지가 1로 있는 경우는 1로 나누어서 어떻게 나누었는지 저장하는 리스트를 따로 만들어 주어야합니다. 그리고 이 리스트를 역순으로 정렬하여
- 1이 저장된 경우 `A`를 제곱한 뒤 `A`를 한 번더 곱하고,
- 0이 저장된 경우 그냥 `A`를 제곱하면 됩니다.
가령, 12가 `B`로 주어졌으면, 빈 리스트인 `multi_form`을 만들고
- 12 // 2 = 6이고 나누어 떨어졌으니 0을 `multi_form`에 `append` (//는 몫을 구하는 연산자입니다.)
- 6 // 2 = 3이고 나누어 떨어졌으니 0을 `multi_form`에 `append`
- 3 // 2 = 1이고 나머지가 1이니 1을 `multi_form`에 `append`
즉 리스트는 `[0, 0, 1]`이 저장이 되었을테고 이를 역배열하여 `[1, 0, 0]`을 만든 뒤, 위의 규칙처럼 `A`에 순서대로 곱해주면 되는 것입니다. 그러면 결과적으로 A^12 가 되겠죠?
하지만, 이렇게 진행을 해도 A^B의 결과로 수가 너무 커질 것을 생각한다면, 역시 메모리 초과가 일어날 수 있습니다. 그래서 역배열된 multi_form의 순서대로 제곱을 해줄 때마다 `C`로 계속해서 나누어 줄겁니다. 그러면 수가 계속해서 커지는 것을 막을 수 있고, 제곱이 되기 전에는 항상 C의 나머지니까 C보단 작아질 겁니다. 그래도 똑같냐고요? 네 똑같습니다. 어떤 수를 제곱하고 `C`로 나누나, 제곱하기 전에 `C`로 나눈 뒤 제곱을 하고 다시 `C`로 나누어도 같습니다(????). 말이 좀 이상한데 정리하면 아래와 같이 됩니다.

음, 이걸 여기에 증명하거나 설명하기는 조금 길어질 것 같아서 생략을 할게요. 대신에 `A`, `B`, `C`를 적절히 설정해서 손으로 몇 문제 풀어보시면 이해가 갈겁니다. 나머지를 구할 때, 나누어 떨어진 부분들에 대해서는 아예 연산에서 제외되는 그런 상황이라고 생각하시면 직관적일 것 같습니다.
아래의 코드로 성공했습니다. 코드가 길지 않고 어렵지 않으니, 어떻게 작동되는지는 가져다가 궁금한 위치에 print해보셔서 확인하시면 더 도움될 것 같습니다.
A, B, C = map(int, input().split())
multi_form = []
while True:
if B == 1: break
if B % 2 == 0: multi_form.append(False)
else: multi_form.append(True)
B = B // 2
# 자주 쓰이는 연산이니 따로 변수로 저장
D = A % C
result = D
for form in multi_form[::-1]:
if form: result = result ** 2 * (D)
else: result = result ** 2
result = result % C
print(result)
'Python > 백준 알고리즘' 카테고리의 다른 글
| [백준 알고리즘: python 3] #1027 - 고층 건물 (1) | 2020.04.18 |
|---|---|
| [백준 알고리즘: python 3] #1026 - 보물 (0) | 2020.04.14 |
| [백준 알고리즘: python 3] #10951 - A + B - 4 (0) | 2020.04.06 |
| [백준 알고리즘: python 3] #1931 - 회의실 배정 (Greedy 알고리즘 스터디) (0) | 2020.04.02 |
| [백준 알고리즘: python 3] #2178 - 미로탐색(BFS 스터디) (0) | 2020.03.25 |
