제가 이번 주부터 친구들과 알고리즘 스터디를 진행하고 있습니다! 이번 주차는 Dynamic Programming(DP)을 공부하기로 했고, DP 문제 중, 1912번의 연속합 문제를 풀기로 하였습니다.
https://www.acmicpc.net/problem/1912
1912번 연속합 문제는 DP의 한 문제로 소개가 되어 있었습니다. 정답률이 높지 않아서, 어려운 문제를 도전하자고 스터디원들과 선택해서 풀게 되었습니다. 저는 DP에 대한 개념을 탄탄하게 알고 있는 편은 아니었고, 개념을 설명해둔 글들을 마구마구 보아도 이해가 잘 안가서 결국 DP로 푸는 문제들을 대부분 포기를 하거나 하는 그런 상황이었습니다. 이번 문제로 DP를 활용해봐서 아 이런 느낌이구나 하는 것을 알았습니다! 이전에 스킵해둔 문제들이 DP로 풀이되는게 있었는데, 다시 도전해볼 법 해졌어요.
Dynamic Programming은 (흔히 재귀함수에서) 반복해서 계산되는 부분들을 다시 계산하지 않고 저장해가면서 다시 계산을 하지 않도록 하여 효율적인 컴퓨터 자원 운용을 목표로 하는 알고리즘 기법입니다. 알고보니 제가 이전에 풀이했던 문제 중, 1003번 피보나치 함수 문제에서 구현했던 피보나치 함수가 Dynamic programming 개념을 설명할 때 자주 언급되더군요. 당시에는 DP의 개념을 모르고 야매로 짜야지 했던 생각으로 코드를 짰었습니다. 아래의 코드죠.
fibonacci = []
for i in range(41):
if i == 0: fibonacci.append(0)
elif i == 1: fibonacci.append(1)
else: fibonacci.append(fibonacci[i-2] + fibonacci[i-1])
40번째의 피보나치 수열을 미리 만들어 두는 부분입니다. 즉, 5번째 피보나치 수를 구하기 위해서 4번째, 3번째 수를 구하게 될 때, 다시 이를 구하기 위해 이전의 피보나치 수를 다시 계산하지 않도록 미리 피보나치 수의 리스트에 저장해두는 것이죠. 이를 메모이제이션이라고 부른다고 합니다. 쉽게 생각할 수 있는 재귀함수를 이용해 40번째 피보나치 수를 구하면 웬만한 컴퓨터는 잠수를 타게 돼요.
그래서 DP를 쓸 때는 점화식이 자주 사용이 됩니다. 이전에 계산된 내용을 불러오기 위해서는 점화식의 표현 방식으로 구현하기 간단하기도 하고, 직관적으로 알아볼 수 있기 때문입니다. DP는 간단히 여기까지 설명을 하려고 합니다. 제 얕은 경험으로 미뤄보아... DP는 천천히 많이 풀어보는게 좋은 것 같아요. 풀면서 점화식으로 표현할만한 규칙을 찾는 것도 중요한 것 같고요.
Hint!
본격적으로 1912번 연속합 문제의 풀이를 설명을 하려고 합니다. 연속합 문제의 설명은 위의 백준 사이트를 참고해주세요. 먼저, 백준에서 주어진 예시를 통해 우리가 결국에 어떤 점화식으로 풀 수 있는지 규칙을 찾으면서 힌트를 얻어보려고 합니다. 문제의 예시에는 아래와 같은 수열이 주어졌었죠?
10 -4 3 1 5 6 -35 12 21 -1
이 수열에서 연속된 수의 합을 고른다고 할 때, 아래의 표로 모든 경우의 수를 구할 수가 있습니다.

(편의상 0번째부터 센다고 합시다.) 위의 표를 볼 때, i번 행의 j번 열의 값이 주어진 수열의 i번 값에서 j번 값을 모두 더했을 때의 값이라고 생각하면 됩니다. 예를 들면 2행 5열에 있는 15라는 값은 주어진 수열의 2번째부터 5번째까지(index=2에서 5까지)에 해당하는 수인 [3, 1, 5, 6]의 값을 모두 더한 값인 것이죠. 밑줄 친 값은 주어진 수열의 수를 나열한거고, 대각선에 놓일 수 밖에 없습니다. 주어진 수열의 i번째 수부터 i번째까지 수의 합은 그냥 i번째 수이니까요!
어떤 규칙이 있을까요? 우선, 표가 그려지는 방식을 생각해봅시다. 3열의 값들은 2열의 값에서 입력받은 수열의 3번째 값을 모두 더한 값입니다. 단, 행과 열의 index값이 같다면 자기 자신이 되는 것이죠. 표를 보면서 이해하면, 2열의 9, -1, 3은 3행 3열의 1(주어진 수열의 index=3의 수)을 각각 더하여 3열의 10, 0, 4를 만들게 되고 자기 자신은 1이 됩니다. 아래 표처럼 말이에요!
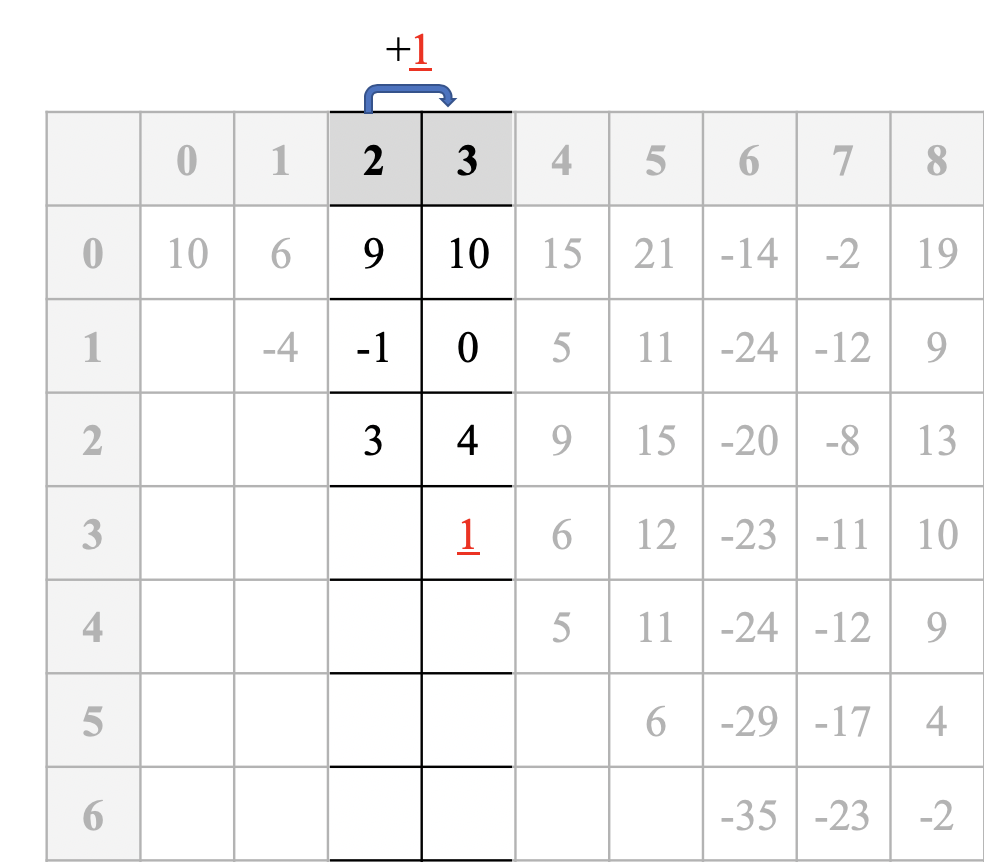
다시 첫번째 표를 봅시다. 첫번째 표에는 굵고 빨간색으로 칠해진 숫자들이 있는데, 그 숫자들은 각 열에서 최대가 되는 숫자를 의미합니다. 즉, 몇 번째 숫자에서 시작을 하든 그 열로 끝나는 연속합을 구한다고 했을 때의 최댓값이 되는 것이죠. 말이 이상하니 예를 들면, 5열에서 최댓값인 21은, 앞의 몇 번째 숫자에서 시작하든 5번째 숫자까지의 연속합들 중 최대가 21이 된다는 것입니다. 결국 문제의 답을 구할 때는, 저 빨간 숫자들 중 최댓값을 구하면 되는 것입니다. 33이 되겠네요.
이제, 이 답을 어떻게 빨리 구할 수 있는지 생각해볼 수 있습니다. 저 표를 일일이 그려서 최댓값을 구하려고 하는 것은 불가능 할 것입니다. 주어지는 숫자의 갯수가 최대 10만개이고, 그렇다면 표는 10만개의 제곱의 사이즈가 되어 계산량이 너무 많을겁니다.
아이디어는 간단합니다. 현재 열의 최댓값은, 이전 열의 최댓값에 현재 열의 대각선의 숫자를 더한 값과 현재열의 대각선의 숫자를 비교해서 큰값으로 바로 결정할 수 있습니다. 5, 6, 7번 열을 보면 이해할 수 있습니다. 6번열의 -14는 5번열의 최댓값인 21에 -35를 더해서 -14가 되어 최댓값이 됩니다. 5번 열의 다른 수를 더해서 최댓값이 될 수 있지 않냐고요? 아뇨! 5번 열의 숫자에 모두 같은 수를 더했을 때 나온 결과 중 최댓값은 5번 열의 최댓값에 더한 것과 같을 수 밖에 없습니다. 반면, 6번에서 7번 열로 넘어갈 때 6번 열의 최댓값은 -14였지만 7번열의 대각선값인 12를 더해도 -2였고 이는 7번열의 대각선 값인 12보다 작아서 자연스레 최댓값 자리를 뺏기게 되는 것이죠. 이 케이스를 보면 제가 설명한 것이 이해가 갈겁니다. 이 과정을 잘 풀어내서 정리하면, 아래의 풀이가 탄생할 수 있어요.
- n 크기의 리스트를 준비합니다. 이 리스트를 dp라고 부릅니다. dp[i]는 위 표에서 i열의 최댓값(빨간 숫자)을 의미합니다. 입력받은 n크기의 수열의 리스트는 num_set이라고 하겠습니다.
- dp[0]은 입력된 수열의 첫번째 숫자인 num_set[0]으로 합니다.
- i가 0보다 크면, dp[i]는 dp[i-1] + num_set[i] 와 num_set[i] 중 큰 값으로 합니다. 즉, 점화식으로 나타내면 dp[i] = max(dp[i-1] + num_set[i], num_set[i]) 입니다.
- 완성된 dp 리스트에서 최댓값을 결과로 출력합니다.
규칙을 알아내고 점화식을 간단히 세워 풀 수 있는 문제였습니다. 이번 문제는 DP문제를 스스로 풀고 설명하는 과정이어서 주저리주저리 생각한 내용을 적느라 난잡할 수도 있을 것 같습니다. 하지만, 저처럼 DP에 익숙하지 않으셨던 분들은 이 설명을 차근차근 읽어보면 이해가 잘 가실거에요! (아마도...)
아래의 풀이로 성공하였습니다.
import sys
n = int(sys.stdin.readline())
num_set = list(map(int, sys.stdin.readline().split()))
# n 크기의 리스트로 dp 초기화
dp = [None for _ in range(n)]
dp[0] = num_set[0]
for i in range(1, n):
# 더한 값과, 주어진 수열의 값(대각선 값) 비교
if dp[i-1] + num_set[i] > num_set[i]:
dp[i] = dp[i-1] + num_set[i]
else: dp[i] = num_set[i]
result = max(dp)
print(result)'Python > 백준 알고리즘' 카테고리의 다른 글
| [백준 알고리즘: python 3] #1874 - 스택 수열 (스택 스터디) (0) | 2020.03.06 |
|---|---|
| [백준 알고리즘: python 3] #1025 - 제곱수 찾기 (3) | 2020.03.03 |
| [백준 알고리즘: python 3] #1024 - 수열의 합 (0) | 2020.03.01 |
| [백준 알고리즘: python 3] #1022 - 소용돌이 예쁘게 출력하기 (3) | 2020.01.19 |
| [백준 알고리즘: python 3] #1021 - 회전하는 큐 (0) | 2020.01.17 |
